Gradient boosting

En intelligence artificielle, plus précisément en apprentissage automatique, le gradient boosting (parfois traduit amplification de gradient en français) est une technique d'apprentissage basée sur le principe de boosting.

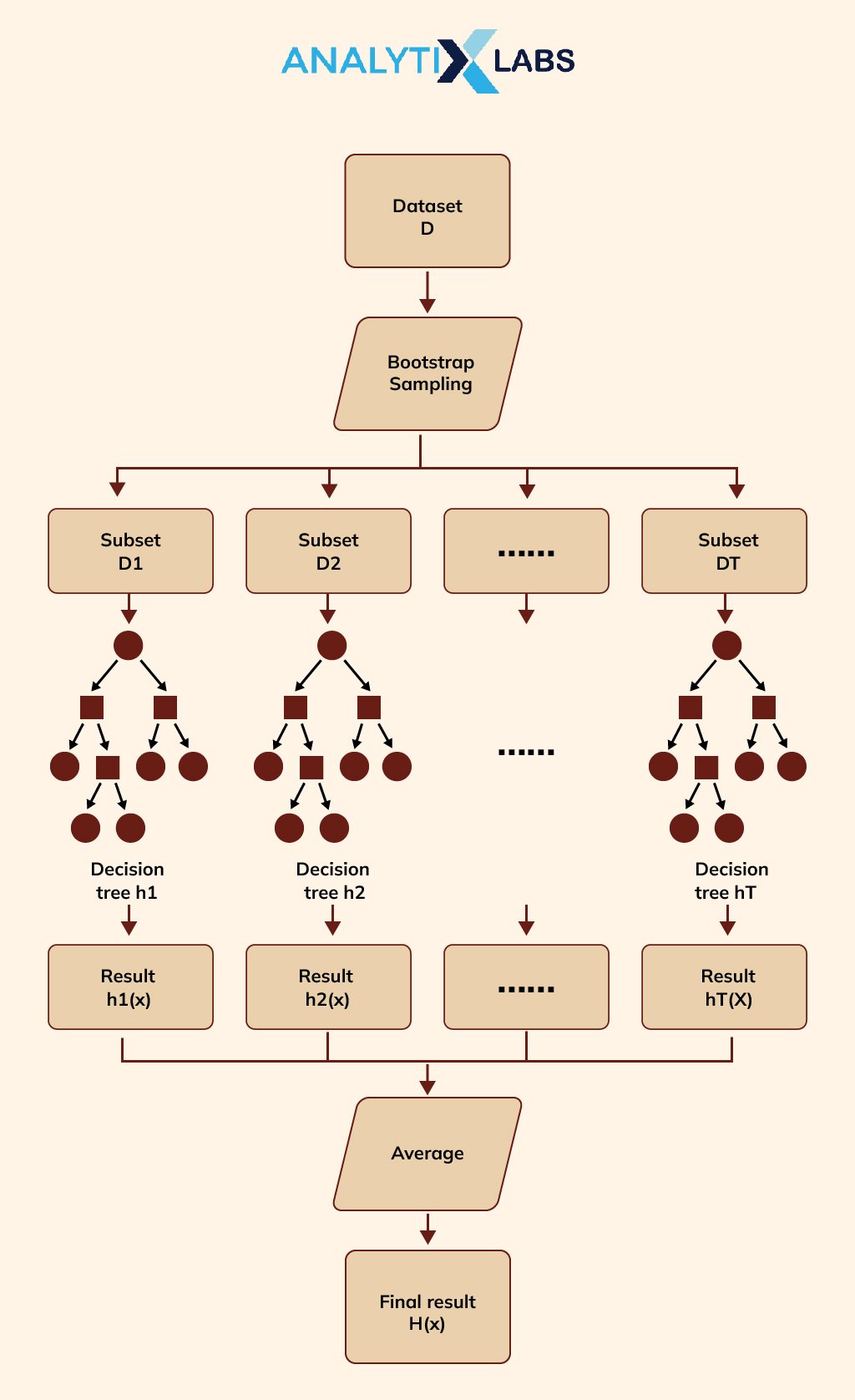
Elle consiste à combiner progressivement des modèles faibles, le plus souvent des arbres de décision, pour former un modèle prédictif performant en corrigeant les erreurs résiduelles de manière itérative. Cette méthode repose sur une optimisation séquentielle où chaque nouveau modèle ajuste ses paramètres en minimisant une fonction de coût via le calcul des gradients. Popularisée par des algorithmes comme XGBoost ou LightGBM (en), le gradient boosting s'impose dans des domaines variés, allant de la recommandation à la classification, grâce à son efficacité et sa capacité à traiter des données structurées complexes.

Historique

Le concept de gradient boosting trouve son origine dans une observation de Leo Breiman datant de 1997, selon laquelle le boosting peut être interprété comme un algorithme d'optimisation appliqué à une fonction objectif appropriée. Des algorithmes explicites de gradient boosting dans un contexte de régression statistique ont ensuite été formalisés par Jerome H. Friedman (en) (en 1999, puis en 2001), parallèlement à des approches plus générales proposées par Llew Mason, Jonathan Baxter, Peter Bartlett et Marcus Frean en 1999^,. Ces contributions ont introduit une nouvelle interprétation des algorithmes de boosting en tant que méthodes de descente de gradient fonctionnel itératif, c'est-à-dire des procédés optimisant une fonction de coût dans un espace fonctionnel en sélectionnant itérativement une fonction (un « classifieur faible ») orientée dans la direction opposée au gradient. Cette perspective fonctionnelle du gradient a ouvert la voie au développement d'algorithmes de boosting dans divers domaines de l'apprentissage automatique et des statistiques, au-delà de la régression et de la classification.

Principe

Cette section suit le tutoriel A Gentle Introduction to Gradient Boosting par Cheng Li (Northeastern University).

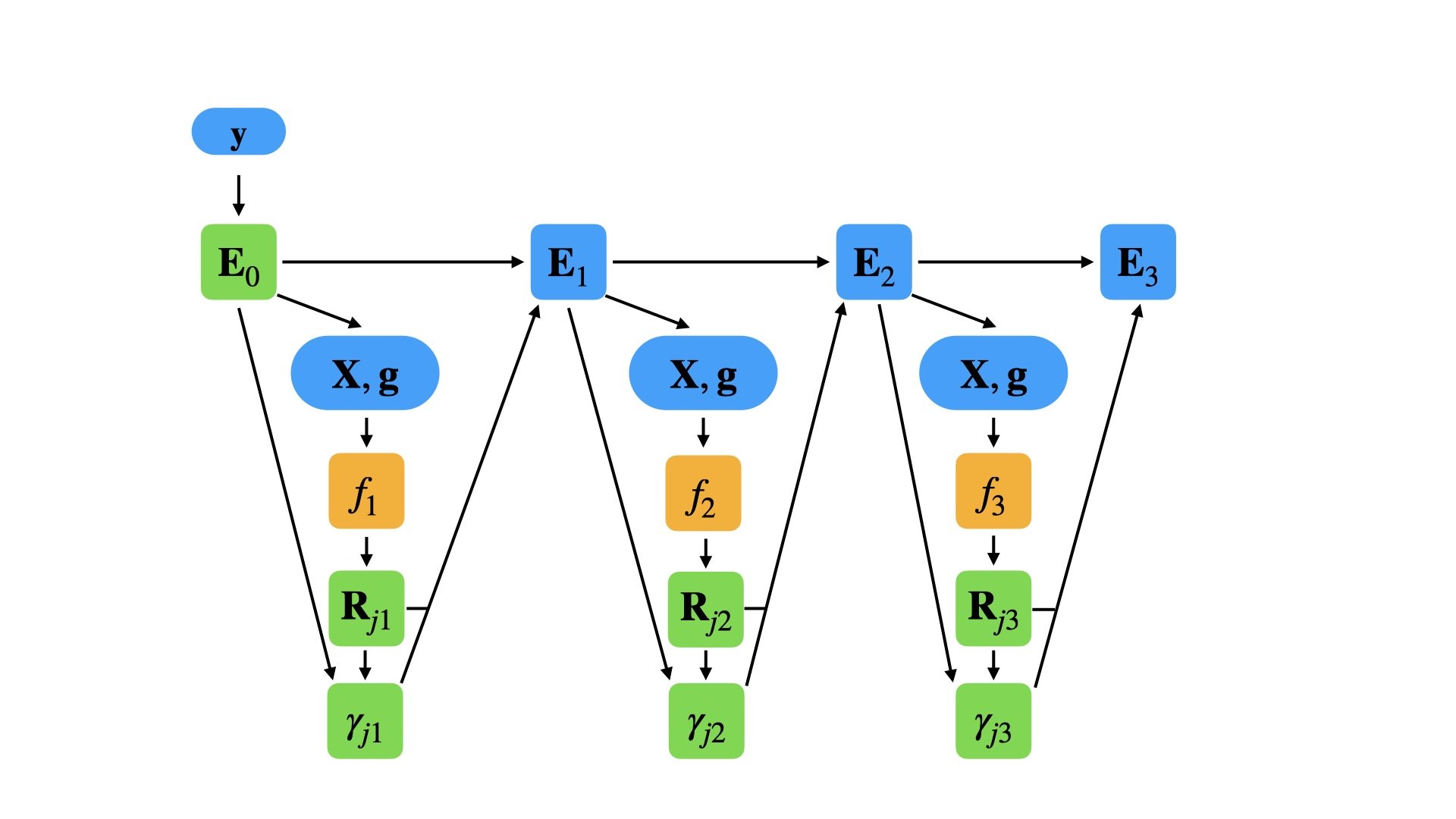
À l'instar des autres méthodes de boosting, le gradient boosting combine des modèles dits faibles en un unique modèle fort par itération. On l'explique ici dans un contexte de régression des moindres carrés. L'objectif est d'apprendre au modèle ${\displaystyle F}$ à prédire des valeurs sous la forme ${\displaystyle {\hat {y}}=F(x)}$, tout en minimisant l'erreur quadratique moyenne ${\displaystyle {\tfrac {1}{n}}\sum _{i}({\hat {y}}_{i}-y_{i})^{2}}$, où ${\displaystyle i}$ est une variable itérée sur un jeu d'entraînement de taille ${\displaystyle n}$, composé de valeurs de la variable de sortie ${\displaystyle y}$ :

• ${\displaystyle {\hat {y}}_{i}=}$ la valeur prédite ${\displaystyle F(x_{i})}$
• ${\displaystyle y_{i}=}$ la valeur observée
• ${\displaystyle n=}$ le nombre d'échantillons dans ${\displaystyle y}$

Si l'algorithme comporte ${\displaystyle M}$ étapes, à chaque étape ${\displaystyle m}$ (${\displaystyle 1\leq m\leq M}$), supposons un modèle imparfait ${\displaystyle F_{m}}$ (pour de faibles ${\displaystyle m}$, ce modèle peut simplement prédire ${\displaystyle {\hat {y}}_{i}}$ comme étant ${\displaystyle {\bar {y}}}$, la moyenne de ${\displaystyle y}$). Pour améliorer ${\displaystyle F_{m}}$, notre algorithme doit ajouter un nouvel estimateur ${\displaystyle h_{m}(x)}$.

Ainsi,

${\displaystyle F_{m 1}(x_{i})=F_{m}(x_{i}) h_{m}(x_{i})=y_{i}}$

où, de manière équivalente,

${\displaystyle h_{m}(x_{i})=y_{i}-F_{m}(x_{i})}$.

Par conséquent, le gradient boosting ajustera ${\displaystyle h_{m}}$ au résidu ${\displaystyle y_{i}-F_{m}(x_{i})}$. Comme dans les autres variantes du boosting, chaque ${\displaystyle F_{m 1}}$ tente de corriger les erreurs de son prédécesseur ${\displaystyle F_{m}}$. Une généralisation de cette idée à des fonctions de perte autres que l'erreur quadratique, ainsi qu'à des problèmes de classification ou de classement, découle de l'observation que les résidus ${\displaystyle h_{m}(x_{i})}$ pour un modèle donné sont proportionnels aux gradients négatifs de la fonction de perte d'erreur quadratique moyenne (par rapport à ${\displaystyle F(x_{i})}$)

${\displaystyle L_{\rm {MSE}}={\frac {1}{n}}\sum _{i=1}^{n}\left(y_{i}-F(x_{i})\right)^{2}}$

${\displaystyle -{\frac {\partial L_{\rm {MSE}}}{\partial F(x_{i})}}={\frac {2}{n}}(y_{i}-F(x_{i}))={\frac {2}{n}}h_{m}(x_{i})}$.

Ainsi, le gradient boosting peut être généralisé à un algorithme de descente de gradient en utilisant une fonction de perte différente et son gradient correspondant.

Usages

Le gradient boosting trouve des applications dans le domaine de l'apprentissage par classement. Les moteurs de recherche Yahoo et Yandex emploient des variantes de cette méthode au sein de leurs algorithmes de classement fonctionnant sur de l'apprentissage automatique. Il est également utilisé en physique des particules pour de l'analyse de données, comme celles du Grand collisionneur de hadrons où des variantes de réseaux de neurones profonds s'appuyant sur le gradient boosting appliquées aux jeux de données ont reproduit avec succès les résultats de méthodes d'analyse traditionnelles, non basées sur l'apprentissage automatique, et ont mené à la découverte du boson de Higgs. Par ailleurs, des arbres de décision utilisant le gradient boosting ont été utilisés en géologie, notamment pour évaluer la qualité des réservoirs gréseux ou pour estimer la profondeur des eaux.

Notes et références

Voir aussi

Bibliographie

• (en) Bradley Boehmke et Brandon Greenwell, « Gradient Boosting », dans Hands-On Machine Learning with R, Chapman & Hall, 2019, 484 p. (ISBN 978-1-138-49568-5, lire en ligne), p. 221-245

Articles connexes

• AdaBoost
• Forêt d'arbres décisionnels
• XGBoost

• Portail de l’informatique
• Portail des probabilités et de la statistique
• Portail de l’intelligence artificielle